[mathjax]みんな~、arcsin(x)の微分がはじまるよ~!!!
ということで早速ですが大まかな手順は、
- 逆関数の微分を活用する
- 三角関数の定義を利用して、簡単な数式に変形する
です。
答えだけ調べに来た方もいるでしょう、
$$\frac{d}{dx}arcsin(x)=\frac{1}{\sqrt{1-x^2}}$$
です。
式変形のまとめは記事の最後の方に載せておきました。
さて今回の記事は、arcsin(x)の微分をより細かく理解していただくこと。
これだけを目標にまとめさせていただきます。
数式が上手く表示されない場合は、何回かF5等の更新ボタンを押してみてください。
逆関数の微分を活用する
そもそもarcsin(x)、sin(x)等の関数は超越関数と呼ばれます。
超越関数とは、四則計算やルートなどで表せない、複雑な関数のことです。
四則計算やルートで表せないからこそ、arcsin(x)、sin(x)のような記号で表します。
そうなるとarcsin(x)の微分もよく分からないので、新しい記号を付けたくなります。
しかし、arcsin(x)の微分を頑張って普通の記号で表そう、とこんな無茶がしたいワケです。
ではどうするかというと、arcsin(x)は定義通り、sin(x)の逆関数であることを利用します。
逆関数はざっくりいうと、関数のグラフのx軸とy軸を入れ替たものです。
グラフの見かけは、直線「y = x」で鏡に映した感じになります。
例えば、
$$f(x)=2x$$
これをxについて解く、つまり「x =」の形にすると、
$$x=\frac{1}{2}f(x)$$
これこそが、f(x)の値をxに対応させる逆関数の正体です。
折角なので求まる側を関数っぽく書きたいですね。
そこでxをg(t)、f(x)をtと書き直します。
$$g(t)=\frac{1}{2}t$$
これで、よく見る関数の形になりました。
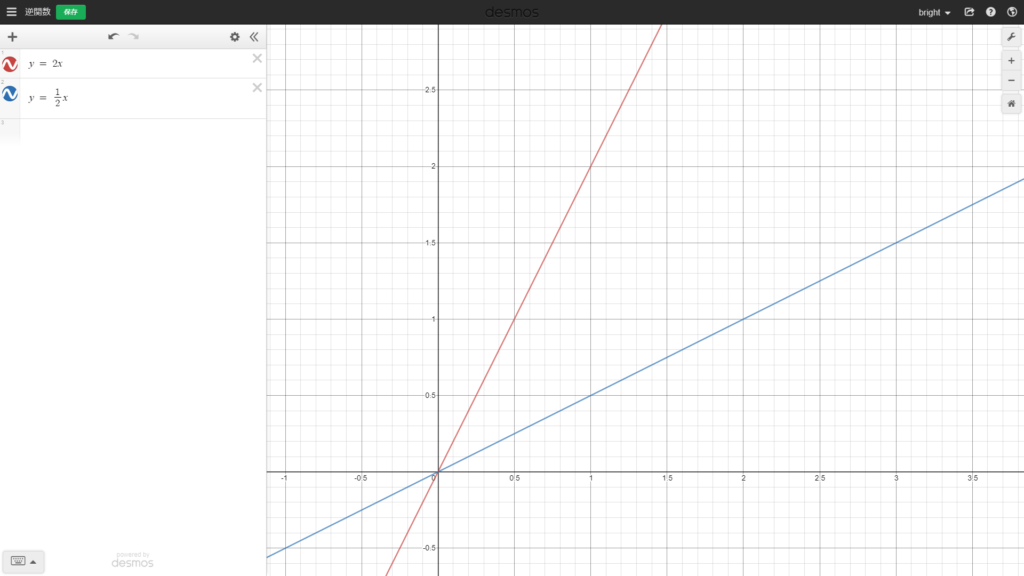
Desmosでグラフを書いてみるとこんな感じです。
ここでのポイントは、傾きがお互い逆数になっている、というところです。
傾きは中学数学でもやるのではないでしょうか。
$$傾き=\frac{yの増加量}{xの増加量}$$
先ほど申し上げた通り、逆関数はx軸とy軸が入れ替わります。
よって、
$$逆関数の傾き=\frac{xの増加量}{yの増加量}$$
分母分子をxの増加量で割ると、
$$逆関数の傾き=\frac{1}{\frac{yの増加量}{xの増加量}}$$
ちゃんと逆数になりますね。
これでまさに、逆関数の微分公式と言われる、
$$\frac{dx}{dy} = \frac{1}{\frac{dy}{dx}}$$
を直感的に示せたことになります。
これにより、逆関数の微分を、元の関数の微分で計算できるようになりました。
つまり今回は、arcsin(x)の微分が、sin(x)の微分で計算できそう、といいたいワケです。
実際にやってみましょう。
$$\frac{d}{dx}arcsin(x)=\frac{1}{\frac{d}{darcsin(x)}sin(arcsin(x))}$$
逆関数なので、微分係数を計算する点も鏡写しになっていることにご注意ください。
つまり元の点(x, arcsin(x))は、逆関数の点(arcsin(x), x)に対応します。
よって、sin(x)の変数xにあたるのはarcsin(x)で、微分もarcsin(x)で行います。
最後に、sin(x)の微分はcos(x)ですから、
$$\frac{1}{\frac{d}{darcsin(x)}sin(arcsin(x))}=\frac{1}{cos(arcsin(x))}$$
と計算できます。
三角関数の定義を利用して、簡単な数式に変形する
arcsin(x)の微分がsin(x)で計算できることが分かり、
$$\frac{d}{dx}arcsin(x)=\frac{1}{cos(arcsin(x))}$$
ここまで変形が出来ました。
これをもっと簡単にするのであれば、arcsin(x)をなんとかしたくなります。
受験勉強でも大事な考え方ですが、式変形は定理があるから、定義だから、ではなく、
答えに近づくための目的に合わせることが重要です。
今回であれば、arcsin(x)などの超越関数をなるべく使わない、これが目的です。
逆三角関数の関係式を利用してもいいですが、他の逆三角関数が出てきそうですね。
ここで選択肢を絞っていくと残るのが、三角関数と逆関数の定義になるワケです。
先ほどの「f(x) = 2x」と「g(t) = 1/2・t」を使ってみましょう。
これらは互いに逆関数なので、
$$g(f(x))=g(2x) = \frac{1}{2}・2x = x\\
f(g(t))=f(\frac{1}{2}t) = 2・\frac{1}{2}t = t$$
このようになり、ある変数に関数とその逆関数を適用すると、変数は元に戻ります。
従って、
$$sin(arcsin(x)) = x$$
という計算が出来るわけです。
これを上手く使えば、逆三角関数を消去出来そうですよね。
それではいってみましょう。
$$\frac{d}{dx}arcsin(x)=\frac{1}{cos(arcsin(x))}$$
を変形します。
cos(arcsin(x))をsin(arcsin(x))に変形できれば、先ほどの計算が使えます。
そこで三角関数の定義、
$$cos^2(x)+sin^2(x)=1$$
を利用しましょう。
元の式にはcos(x)しか存在しないので、cos(x)について解くと、
$$cos^2(x)=1-sin^2(x)$$
となります。
2乗では代入できないので、1乗にするためにルートを計算します。
ルートの計算は正の平方根と負の平方根の2つを伴うので、間違えないように選びましょう。
実はarcsin(x)の定義から、
$$\frac{-\pi}{2} \leqq x \leqq \frac{\pi}{2}$$
であるため、
$$cos(x) \geqq 0$$
です。
よって正の平方根である、
$$cos(x)=\sqrt{1-sin^2(x)}$$
を利用します。
さぁ代入してみます!
分母が0の時は微分係数が定義されないので、「cos(x) = 1」など気にせず代入しましょう。
$$\frac{1}{cos(arcsin(x))}=\frac{1}{\sqrt{1 – sin^2(arcsin(x))}}$$
そして逆関数の定義より、
$$\frac{1}{\sqrt{1 – sin^2(arcsin(x))}}=\frac{1}{\sqrt{1 – x^2}}$$
となり、はれて超越関数を使わずに、arcsin(x)の微分を表すことが出来ました!
式変形のまとめ
\begin{eqnarray}\frac{d}{dx}arcsin(x)&=&\frac{1}{\frac{d}{darcsin(x)}sin(arcsin(x))}\\
&=&\frac{1}{cos(arcsin(x))}\\
&=&\frac{1}{\sqrt{1 – sin^2(arcsin(x))}}\\
&=&\frac{1}{\sqrt{1 – x^2}}\end{eqnarray}
この式変形を見ながら、1行1行理由を思い出してゆくと理解が確認できると思います。
忘れてしまった場合は記事を読み返してみてください。
あれだけの理屈がこの4行に集約されるという事実に、どこか感動を覚えませんか?
そんな説明で大丈夫か?
逆三角関数の微分を勉強したとき、私自身多くの記事を参考にさせていただきました。
そんな記憶から、こんな紹介もアリなのでは、という要素を詰めこんだのがこの記事です。
数学の解説でありがたいのはなんといっても、式変形が詳しいことに尽きるでしょう。
しかし、数式という抽象化を施した時点で、式変形は正解不正解が明確です。
なので式変形という情報は、理解が正しいかどうかを確認するものであって、
理解を得るために必要な情報、という側面は薄くなることが多いです。
そうなると、理解が出来ていない人に必要なのは何か。
ズバリ、式変形における目的の意識なのではと考えました。
- 証明の式変形で、1つ1つの等号にどのような前提を使ったのか
- 計算の対象が何で、前提となる公理はどれか
などの式に現れない部分は、計算規則と違って文脈にゆだねられることが多いです。
この文脈の判断ミスが、「三角形だと思っていたら四角形だった」ならまだいいでしょう。
おそらくあなたに起きているのは、
「連続だと思っていた関数に不連続な点があった」というレベルのミスです。
不連続な点では片側極限は定義されますが、極限値は存在しませんし、微分も出来ません。
という具合に知識を対応させられるか否かが、数学の理解度なのかな、と思うわけです。
長々となりましたがまとめます。
今回の記事では、
「arcsin(x)を微分するため、これまでに学んだ分野をどう組み合わせるのか」
ということをこと細かに書いてみました。
高校数学より先の範囲は習う人も少ないせいか、情報量も少なく学習に手間がかかります。
こんな記事ですが、数学が得意になりたい人の助けになれば幸いです。
はぁことこ。


コメント